Introduction
Given that Quentin Meillassoux’s After Finitude (AF) is a work that explicates the notion of ‘speculative realism’ and calls for a new direction towards which continental philosophy should turn, it does not however offer a positive theoretical framework, but rather, relies on allusions to Alain Badiou’s work Being and Event (BE). In numerous ways, Meillassoux relies on Badiou’s mathematical ontology in order to derive one of the most crucial notions of ‘absolute chaos’ and ‘factiality’ which posit the necessity of contingency of all natural laws. Based on this problematic, Meillassoux attempts to come up with terms such as the ‘arche-fossil’ and ‘ancestriality’ in order to set out the problematic that a project of speculative realism must revolve around. To various extents, these questions can only be derived indirectly from Badiou’s BE since this work deals with an ontology grounded in set theory as apposed to the rather more empirical and practical questions regarding how science can absolutely ground the validity of ancestral statements as they are posed in Meillassoux’s AF. Meillassoux work can be seen as one that takes up Badiou’s ontology in conjunction to the problematics encountered by Descartes, Kant and Hume and posits a new problematic in a manner that puts forward a more concrete question regarding what should really be at stake in contemporary philosophy, which in turn, very much constitutes the problematic posed by the ‘speculative realist’ project. With this in sight, the manner in which Badiou’s ontology is translated and implicated in Meillassoux’s AF will be the characterized focus of this paper’s discussion. The first theme concerns Badiou’s notion of the event and its relation to the active subject along with its potential relation in Meillassoux’s AF. The second theme that will be discussed regards Meillassoux’s notion of ‘absolute chaos’ and its relation to Badiou’s notion of the void set that is derived based on Cantors set theory. Lastly, the implications of Meillassoux’s allusion to Badiou’s set theory in order to ground one of the most crucial terms for the speculative realist project, will be the theme discussed more broadly.

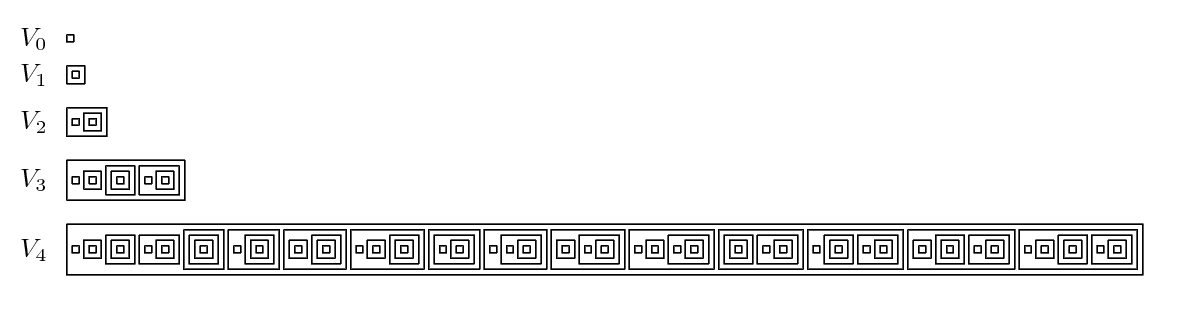
fig.1: A depiction of a fractal based on the Mandelbrot set, a progressive mathematical sequence that entails infinite iterations no matter how small or big the scale of the illustrated sequence is. This illustrates one of the outcomes of Badiou’s ontology based on pure multiplicities and iterative sets, an outcome which is counteracted and argued against with Badiou’s notion of ‘void’ and Meillassoux’s notion of ‘absolute chaos’—positing that reality is not infinitely recursive, but rather, consists of an ultimate bedrock compromised out of chaos or the ‘void-set’ (denoted as {∅}).
The Paradox Between two Thesis
To commence the exposition of the promised themes, it will first be helpful to start with a discussion on an impasses that arises in Badiou’s BE. This impasse concerns one of the most crucial notions of Badiou’s BE regarding the ‘event’; it will then hopefully serve as a bridge that transitions to what is most crucial in Meillassoux’s AF which entails the ‘speculative realist’ project and the critique of ’correlationism’; then finally, this will serve as the basis to investigate the most important aspect of what BE and AF both share in common: the notion of ‘void’, ’absolute chaos’ and ‘necessity of contingency’. The first paradox that arises is between two thesis in Being and Event. The first thesis is the following 1:
Situations are nothing more, in their being, than pure multiplicities. If truth exists, they are certainly indifferent to differences (BE, xv.1).
And the second thesis:
An event takes place and what remains in the form of strictly incalculable emergence (BE, xv.2).
In claiming that “If truth exists, they are certainly indifferent to differences”, Badiou suggests that there are truths which are quasi-irrelevant to their manifestations in physical reality, just like the universal Platonic Forms are indifferent to their particular manifestations; however, in his theory, Badiou also demonstrates that an ontology of any given situation and its manifestation in reality can be inscribed and determined based on Cantor’s set theory. In this sense, Badiou shares something similar to Plato in that their idealist philosophies have almost no direct relation to reality, but on the other hand, they rather paradoxically reveal something ontologically fundamental and concrete about this very reality: the nature of its being (as in “Being and Event”). This precisely demonstrates Badiou’s motivation to bridge philosophy with mathematics and geometry as it had been in the times of Plato, but instead of mathematics, Badiou bridges his philosophy of ontology with Cantor’s set theory instead. As Badiou claims:
Set theory, considered as an adequate thinking of the pure multiple, or of insofar as it reflects the latter’s being as such; that is, the multiple of the presentation of presentation, formalizes any situation whatsoever multiples which makes up any presentation.2
On the other hand, and this concerns the second thesis of the paradox mentioned above, Badiou also introduces a notion that escapes all ontological determinacy and totalizability of any given situation or system that attempts to predicate it, even while being included within the ontological framework derived from Cantor’s theory of mathematical sets: such notion is what Badiou refers to as the ‘event’ (as in “Being and Event”). Given that Badiou seeks a quasi-Platonic return to mathematical formalism whose aim is to recuperate its hospitable relationship with philosophy in an attempt to derive the absolute ontological foundation of any given situation that manifests itself in reality; it at the same time however, conceives of a notion that would always remain outside the totalizability of its own system, which is precisely what the notion of the event implies. Hence, the paradox is in the fact that an ontological framework can inscribe and determine the conditions of possibilities of all its elements and multiplicities, yet, the same cannot be said about the event, which escapes all determinacy. It is a concept that escapes every ontological framework that attempts to contain it, including the formalities and conceptual frameworks that we, finite reasoning subjects invent, who attempt to grasp, explain and totalize encountered phenomena, while always striving to some Platonist, Cartesian or Hegelian notion of universality, objectivity and absolute.
Given this feature inherent in the event—that which always remains outside the processes of inclusion—a tension seems to arise with Meillassoux’s project of ’speculative realism’ as expounded in his After Finitude (AF)3. If one seeks to establish a philosophical framework that attempts to formalize reality on a universal, mathema-ontological foundation in a manner that finally achieves the reconcilement of “being and thought”4 as a manner of resolving the plague of ‘corelationism’ that being and thought was dragged on by continental philosophy since Kant; then how can this realism succeed if it already admits of what it cannot ascribe? Even though Meillassoux sees the possibility of accounting the casual emergence of physical phenomena, ‘arche-fossil’ statements, and emergence as such, under what he deems as a promising formal mathematical framework offered by Badiou, how can the fact that something like the event which escapes all methods of formalization and totalization—be an inherent aspect of the ‘speculative realist’ project that Meillassoux is pursuing? Moreover, the implication of Meillassoux’s thesis of ‘necessity of contingency’ makes this problem more challenging since it posits that nothing is certain, even the laws of physics, the laws of causality and even the principle of non-contradiction can, at a certain moment, become falsified due to the fundamental contingent nature of reality.
Therefore, the question then arises regarding how can the radical contingency of reality along with the untotzlizable spontaneous emergent nature of the event, be reconciled with an an ontology that promises some axiomatic determinacy? As the outcome with anything conceived under Badiou’s set theory, the answer to this question is multiple; but at least two ‘multiples’ of this question will be emphasized. These two points surround the most important aspect which concerns the manner in which Badiou’s mathematical ontology leaves room for spontaneity and emergence of the event but not on the grounds that are associated with someone like Kant, who grounds free will based on the capacities of finite human reason, which also famously lead him to leave some room for faith, etc.; but rather on something that is ontologically fundamental to reality itself. For Badiou and Meillassoux, this fundamental bedrock of reality consists of the notion of void, which concerns the latter second point. While the first point regards Badiou’s attempt to re-imagine the capacities of a philosopher as an active subject, who possesses the agency to discover the a priori nature of reality consisting of pure multiplicities as derived from Cantor’s set theory—and be able to practically alter reality itself—but at the same time, not be susceptible to Meillassoux’s critique of Kantian correlationism, where the relativism between thought and being prevails, and no absolute, a priori ground can persist when thought is separated from the being who thinks it. Therefore, the subject must on one hand have some agency think and apprehend the world, but not to the extents that this process becomes to contingent on thinking and being, which makes it risk becoming anti-realist.
∈, ⊂, State and Situation
The way in which Badiou formulates the importance of the subject as an interpreter of any given state or situation, occurs as a bridging of the impasse between two operators: belonging (∈) and inclusion (⊂)5. As Badiou summarizes, the two main forms of metaphysics that prevailed in philosophy, are the overarching binaries between the ‘One’ and the ‘Multiple’ manifested in the oppositional views between Plato and Aristotle6. What set theory offers instead, is an ontology that conceives of everything as a relationship between pure multiplicities, thus dismantling the traditional binary opposition in philosophy between the One and the Multiple. Thus, the two most important operators that help to determine the relationship between multiplicities are belonging (∈) and inclusion (⊂) where the distinction between them lies in that the former means that one is counted as an element within a set that determines the procedure of ‘count-as-one’, whereas the later is an inclusion that resolves in both the element and the set within which it is counted to have a relationship that is pure multiple and therefore also reversible. It is precisely in this gap between belonging and inclusion within a given state or situation that makes the subject riveted to the situation one belongs to; while on the other hand, having the agency to overcome this imposed belonging to a given situation and alter the very process of relationship of this belonging. This therefore also translates into a theory of multiplicities that is not purely determinist and realist that essentially extinguishes all free will and agency, but one that can nevertheless be realist while also leaving room for a subjective force that leads to the event—that which ruptures altogether the relationship of belonging and inclusion among multiplicities that together constitute a state or a situation, causing an emergence of ‘new truths’ and relationships among multiplicities. It is precisely in this sense that thought and being are on one hand, correlated in the sense that gives the subject the autonomy to interpret and change its situation, while on the other hand, the subject is already inscribed within a realist mathematical ontology from which realist truths independent from the subject itself can emerge, be derived and inscribed. This can explain why Meillassoux sees a realist potential in Badiou’s set theory even if Badiou’s notion of the event might be immediately seen as an anti-realist element if this very ontology.
For Badiou, while avoiding the forms of subjectivism of modern philosophy, attempts to delineate an ontology through which the subject emerges out of an event rather than being contingent to a predetermined structure of being (DBB, p. 111). It is precisely in this aspect of Badiou’s mathematical ontology and Meillassoux’s ‘speculative realism‘ seeks to ground their ontological realism on, where on one hand, the subject is no longer a quasi-transcendental bridge for the correlation between thought and being—as is predominant in Kantian, correlationist philosophy; but on the other hand, the subject itself rests casually undetermined and untotalizable by the realist framework within which it is inscribed. In describing the implications of Badiou’s ontology, Meillassoux states that “what the set-theoretical axiomatic demonstrates is at the very least a fundamental uncertainty regarding the totalizabity of the possible…We have no way of knowing whether the possible can be totalized in the same way as the faces of a set of dice can be totalized”7. This ultimately resonates with the entailing importance of the subject who can theorize the world according to both thinkers: as Badiou writes in the “Preface” of Meillassoux’s AF, the philistine subject in its renewed quest for truth must ultimately pose a first-person Kantian question: “what can I know?”.8 This emphasis on the subject to various extents, is differentiated from the Cartesian cogito, where the subject no longer uses its own existence as a predicate for thought, but rather, has the inherent agency to predicate an axiomatic, mathematical understanding of reality in a manner that can derive and ground a project for a realism, as that of Meillassoux’s, who attempts to overcome the ‘correlationism’ between being and thought. One of the theoretical concepts that both thinkers share as an attempt to detach from philosophy’s obsession with the predicate of being is through the conception of ‘non-being’ which is that which cannot be ‘counted-as-one’, along with the conceptions of ‘void’ and ‘absolute chaos’. It is the exposition of these ontological themes that provides the subject the capacity to conceive a realism that is no longer predicated on one’s own being, but one that can become predicated based on the imagined possibility of one’s own non-being. In this way, fundumental ontological truths are constructed trought the notion of non-being. With a resonance with the revolutionary politics of his early period, Badiou elaborates on the function of the subject as a thinker striving towards truth:
The militant of a truth is not only the political militant working for the emancipation of humanity in its entirety. He or she is also the artist-creator, the scientist who opens up a new theoretical field, or the lover whose world is enchanted. (BE, p. xvi)
Ultimately, Meillassoux abstinence from including Badiou’s notion of the event in his own ‘speculative realist’ project might be a matter of caution in regards to the translation of political commitments onto his own philosophic project, unlike Badiou, who does not entirely dispense his past commitments to Maoism while elevating them to a more materially abstract, yet more ontologically concrete plane that becomes grounded in set theory. It is precisely in this theory of multiples that allows a subject to alter the configuration of the very situation within which it is inscribed while also being inscribed under a pseudo-realist mathematical ontology. This translates into certain political repercussions for example, where the law of ‘count as one’, instead of being a reciprocal relationship between pure multiples is instead dictated by the State trough a totalizing force of belonging (∈) over its subjects without offering some (or most) of its subjects the agency to decide how this process of belonging occurs9. Thus, the resolution of this antagonism would entail the subject dictating the process of this belonging, which would at the end, cancel out the process of belonging that was previously dictated solely by the State. Therefore, the result resembles a democracy where citizens are pure multiples of the State, and the State is a pure multiple of its citizens, thus becoming an inclusion (⊂) instead of mere belonging (∈); however for Badiou, this entails a dictatorial kind of democracy, where all citizens exercise their dictatorship over the State in order to pursue their collective interests. Thus the citizens as individual subjects, are no longer solely belong (∈) to the State, but are also included (⊂).
Set Theory contra Correlationism
As Crockett suggests10, Badiou’s mathematicized ontology of being does not attempt to prescribe the event as a irreducible mathematical multiplicity, but rather, prescribes the conditions of possibility under which such a un-totalizable event can occur (DBB, pp. 5-6). A few paradoxes emerge in both Meillassoux’s and Badiou’s stances as well, which both thinkers are extensively aware of; even if both thinkers are to various extents anti-correlationist, anti-Kantian, quasi-Cartesian, quasi-Platonist and Humean skeptics, Badiou’s ontology ends up being quasi-Kantian insofar as it is obsessed with offering an ontology capable of formulating the conditions of possibility of an event while resembling Kant’s project in the Critique of Judgment attempting to bridge pure reason and practical reason (DBB, pp. 104-5); while Meillassoux’s realism attempts to grapple with the remnant of ‘correlationism’ present in Cartesianism, even if Meillassoux deems Descartes as the exemplary on which the speculative realist project must draw on—in conjunction to a reading of Hume who proposes a radicalization of contingency of the laws of nature. However, Meillassoux’s main critique against Descartes’s attempt to ground absolute knowledge—based on an ontologically proven, ‘clear and distinct’ conception of a supreme being—is that it does not prove “the existence of the absolute, because the necessity it affirms is merely a necessity for us”11. It is in this sense, what Meillassoux traces is a remnant of correlationism in Descartes’s thought where the cogito serves as a predicate for a philosophic system.
Even if Descartes proves the existence of God that grounds the faculties of the mind to ground the realism of his ‘First Philosophy’, it hints on a remnant of correlationism, which makes Descartes’s argument easily susceptible to Meillassoux’s own polemic against correlationism. Meillassoux does however draw on the philosophical procedure that he deems crucial in the Cartesian ontological proof of God, where the supreme being serves as a mediator grounding the cogito’s (mind’s) capacity to apprehend the existence of extended substance in physical reality—absolutely. Despite this, Meillassoux does acknowledge that Descartes’s proof is susceptible to a critique directed towards its circularity, known as the ‘Cartesian Circle’12 : Descartes claims that he can prove God’s existence through ‘clear and distinct’ ideas, though he also claims that he can only derive ‘clear and distinct’ ideas after he has proven God’s existence. With this in mind, Meillassoux seeks to avoid such circular argumentation by proclaiming “we must uncover an absolute necessity that does not reinstate any form of absolutely necessary entity”13. It is precisely at the point that ‘absolute chaos’ and the notion of ‘void’ become necessary concepts that substitute the necessity of an existing Cartesian God.
If in this sense, Meillassoux takes inspiration from the Cartesian procedure of grounding a realism by demonstrating how the finite faculties of the mind can gain the capacity to partially grasp reality in its absolute form, while however, dispensing the necessity of the existence of God in favor of the necessity of ‘absolute chaos’; while Badiou, being and avowed atheist, takes a parallel inspiration from Cantor’s set theory while dispensing Cantor’s conclusion that his set theory points to an absolute infinity that can be referred to as ‘God’ (DBB, pp. 108). While Meillassoux draws on the Cartesian procedure while pointing out the remnant correlationism still being prevalent in this theory; Badiou takes a more radical reproach against Cartesianism in taking a route against all forms of subjectivism that have plagued modern philosophy, which serve as the motivation for establishing the grounds of his mathematical ontology based on Cantor’s set theory through the so called “nine canonical axioms“: extensionality, union, separation, replacement, foundation, the infinite, choice, and most importantly for the theme to be developed below in this essay—void (DBB, pp. 107). Despite all the axioms, Badiou also leaves room for the notion of the event.
In light of the various paradoxes that emerge in Badiou’s BE and Meillassoux’s AF, both converge in one important aspect, where instead of offering a positivistic framework within which the speculative realist project of the former and the mathematical ontology of the later can carry out their practical application—the works of both thinkers, rather resemble projects that establish a discursive field offering the conditions of possibility within which their projects can further evolve and develop, if not resembling manifestos that are ellaborated rather notably well, especially in the case of Meillassoux’s AF. Both thinkers however, share a common regard to one of the most crucial convergences between Badiou’s and Meillassoux’s canonical works to be delineated and emphasized below, which is the philosophic concept of ‘absolute chaos’ and ‘void’ that, rather paradoxically, act as crucial foundations for the positive frameworks that both of the theorists put forward.
Something from Nothing: V∅id and Absolute Cha∅s
Travel down into this coffee cup—through the milk particles, down to the atomic level and right down to the sub-atomic level, and you enter a world where conjuring something out of nothing is possible.14
Because Meillassoux’s and Badiou’s motivations can be generally regarded as an attempt to bridge the most crucial impasses that existed in modern and even latently in pre-modern philosophy, namely, between thought and reality, mathematics and reality, contingency and necessity, theory and practice, etc; a fundamental question arises in regard to reality as such, its nature, and—a question that both thinkers believe to be crucial rather than being solely a matter of philosophic entertainment: a question posed by Leibniz as “Why is there something rather than nothing?” For both Badiou and Meillassoux, the answer is quite paradoxical: the condition for something is precisely that pure nothing prevails in reality, whether that is ‘absolute chaos’ for Meillassoux, or the ‘empty set’/‘void-set’ (denoted as {∅}) for Badiou. Badiou further elaborates the notion of ‘void’ must be more closely understood according to the Greek conception of the term that takes it as a ontological category rather than a experimental difference derived through a mathematizable mediation of measure as it is prevalent following the Galilean revolution15. The condition for the emergence of something is either chaos, or nothing for Meillassoux; as Badiou sums up, the “being of consistency is inconsistency” (BE, p. 56). In “Meditation 7” of BE, Badiou offers a ‘Universal formula for inclusion of void’ which proves on the basis of set theory that the basis of every multiple set, is a void set that contains nothing but void itself.16 The formulation of the formula for this universal inclusion of void in all multiples can be written as (∀N)[∅ ⊂ N] where given any existing (operator ‘∀’) multiple called N, void (∅) is included (⊂) within N. This demonstrates that at some point, there is void set ({∅}) consisting of nothing but void as its element (∅) included in any given multiple N. Thus proving that the basis of all multiplicities is void.
In the chapter “The Principle of Factiality” in his AF, Meillassoux sets out the notion of ‘factuality’ by first defining it as a “non-facticity of facticity”17 where ‘facticity’ itself consists of “the minimal organization of representation” of various facts and logical propositions about the world—not yet elevated to a universal, absolute status18. Meillassoux’s seeks to ground a universal statement based on a fundamental quality of facticity itself, where the laws according to which this facticity occur, can themselves change at any given moment. Thus opens up the procedure that Meillassoux follows based on Badiou’s formula: “being of consistency is inconsistency” (BE, p. 56). What allows the constitution of this movement is the grounding of an absolute in the notion of ‘unreason’, ‘Chaotic absolute’, and the conceivability of death and ‘non-being’ —under a concept referred to as the ‘principle of factiality’. By doing so, Meillassoux first provides an argumentation that absoluticizes ‘unreason’ and ‘absolute chaos’, which in Badiou’s terminology would entail the necessary inclusion of the ‘void-set’ in all multiplicities. For Meillassoux, even the most intuitive laws such as the principle of non-contradiction, become contingent to the mathemetical nature of reality: “it is no longer the logical principle of non-contradiction that is absoluticized, but rather the mathematical statement qua mathematical”19.
This therefore entails the general project that both Meillassoux and Badiou share, it is not necessarily a possibility of accessing the absolute, but demonstrating the field in which the absolute dwells by acknowledging the possible limitations that lie in the attempt of such access. It is precisely at this point that the role of subject plays a constituting role in interpreting and forming new situations in which truths can be formed and brought forward. Meillassoux then asks, how can then “Chaos possibly legitimate knowledge of the ancestral?”20 First, the notion of non-contradiction is still a crucial component for grounding any access to the absolute, since without it, it becomes nearly impossible to make sense of anything; but paradoxically, the basis of non-contradiction becomes the chaotic absolute itself, which also removes the requirement for a existence of a necessary being.21 Second, in an attempt to answer the Leibnitz’s question “why there is something rather than nothing?” without resolving into fideist belief that the world was gifted to us and whose absolute outdoors always remain inaccessible,22 Meillassoux proclaims that it is necessary that something exists, because it is necessary that contingent things exist.23
The Nature of Reality under The Theory of the Multiple
Following the explanation of what constitute the concept of void and how something arises out of it, arises another question regarding material reality and how it arises out of this very void. Void is the fundamental theme of Badiou’s ontology in its finality, in the atomist sense of the word—where instead of the atom, the backbone of material reality consisting of pure multiplicities—is ‘void’ (BE, p. 61). Since every multiple is composed of multiples, ultimately within the hierarchy of multiplicities and sub-multiplicities (or sets and sub-sets), one can ultimately derive a multiplicity that consists of a void or a ‘void-set’. The ‘void-set’ or ‘empty-set’ is therefore the fundamental basis of multiplicities of multiplicities, but since there can be no element inscribed within a set that is not a member of a parent set—unless it is a void set ({∅}) consisting of nothing but void(∅)—then it follows that void is included (⊂) in all multiplicities and sets (BE, “Meditation 5”, p. 72). This also amounts to that there is no such thing as an element existing outside of a multiplicity; only void as such can exist with a parent set that predicates it, resulting in void being the fundamental basis of every multiplicity. The pure multiple is therefore void, pure nothing.
However it may be pointed out that the supposition positing that ultimately, the basis of all hierarchies of sub-sets within sets (within sets within sets and so one)—is void, pure nothingness and absolute chaos—lies on the supposition that these hierarchies are not infinite and that ultimately there is a bedrock consisting of void. Such response would posit that perhaps, reality is infinitely recursive, consisting out of infinitely recursive sets, resembling a Mandelbrot fractal (fig.1), the span of which is infinite. This would ultimately posit that the bedrock of material is not void as such, but an infinitely recursive reality. Although such a conclusion can be derived from Badiou’s ontology, whether reality consists of infinitely recursive multiplicities rather than a bedrock consisting of empty sets consisting of nothing but void, entailing a “the unrepresentable that to which nothing, no multiple belongs” (BE, p. 72)—does not however impede Badiou’s mathematical ontology that posits that reality consists of nothing but multiplicities and sets.
In Badiou’s ontology, material reality therefore consists of void where void is matter conceived qua matter (BE, p. 75). This therefore entails a physical reality that can be reduced into multiplicities until its underlying backbone is encountered in the form of void, or cannot be reduced to anything. As put by Tilford:
The ontological multiples in themselves are deprived of the order manifested for us in the empirically given: they are only multiples composed in their turn of multiples. A building is a multiple of bricks, which in turn are a multiple of molecules, made of a multiplicity of atoms, themselves decomposable into a multiplicity of quarks – and so on to infinity, since the ontology of Badiou does not hold to the data of current physics – to make of any entity a pure multiple in which no fundamental unit is ever encountered.24
The relational outcome between Badiou’s ontology and material reality itself, as Crockett critically points out, is a philosophical understanding of the world that is “big, slow and cold” as opposed to one that attempts to grasp the fast-paced “fundamental world” consisting of particle physics, minuscule Planck scales (DBB, pp. 103), and the wave functions of sub-atomic quantum phenomena. This is a result of Badiou’s framework that is critically referred by Crockett as a “frozen ontology” resulting from its reliance on static and axiomatic forms of mathematics. However, considering Tilford’s prior remark, due to Badiou’s reliance on sets of multiplicities that can account as many recursive multiplicities deemed necessary to inscribe the fast-paced “fundamental world” of physical reality, Badiou’s ontology is able to absorb this critical remark.
_[AF]: Meillassoux, “After Finitude: An Essay on The Necessity of Contingency” (2008) _[BE]: Badiou, “Being and Event” (2005) *[SSR]: Kuhn, “The Structure of Scientific Revolutions” (2012)
-
BE: Alain Badiou, trans. Oliver Felthaam; Being and Event (New York: Bloomsbury, 2005, 2006, 2007, 2015, 2016). ↩
-
BE, “Meditation 12”, p.136, (emphasis my own). ↩
-
AF: Quentin Meillassoux, trans. Ray Brassier; After Finitude: An Essay on The Necessity of Contingency (New York: Bloomsbury, 2008). ↩
-
AF, p.128 ↩
-
BE, “Meditation 8”, p.105 see “Meditation 7.1”, pp.86-7 as well. ↩
-
BE, “Meditation 7.1”, p.85-7. ↩
-
AF, p. 105. ↩
-
Meillassoux, “Preface by Alain Badiou”, After Finitude, p. vii. Alluding to Kant’s Critique of Pure Reason (A:1781/B:1787). ↩
-
BE, “Meditation 9”, pp.109-111. ↩
-
DBB: Clayton Crockett, Deleuze Beyond Badiou: Ontology, Multiplicity, and Event (New York: Columbia University Press, 2013), ↩
-
AF, p. 30. ↩
-
In all fairness, Descartes also is aware of this problem and offers a possible way out in his responses in his Meditations. ↩
-
AF, p. 34. ↩
-
Stephen Hawking, Brief Answers to the Big Questions (New York: Bantam Books, 2018), p.33. ↩
-
BE, “Meditation 6”, p.76. ↩
-
BE, “Meditation 7.3”, p.96. ↩
-
AF, p. 79. ↩
-
AF, p. 39. ↩
-
AF, p. 81. ↩
-
AF, p. 65. ↩
-
AF, pp. 71, 67. ↩
-
AF, p. 72. ↩
-
AF, p. 74. ↩
-
https://larvalsubjects.wordpress.com/2008/08/13/meillassoux-on-badiou/ ↩